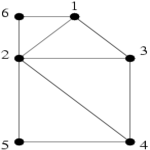
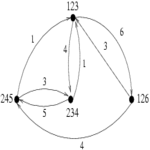
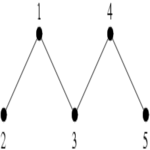
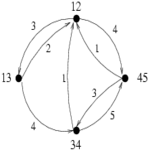
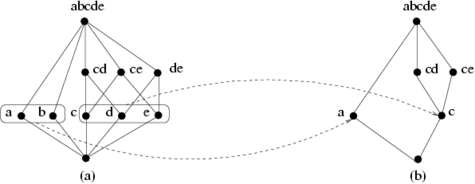
Ci-dessous, deux graphes et les graphes de transitions de leur famille de cliques maximales
Affiliation : LITA, Equipe Algorithmique et Optimisation.
Ci-dessous, deux graphes et les graphes de transitions de leur famille de cliques maximales




Algorithmique, Enumération, Combinatoire, Structure Discrètes, cliques, bicliques, systèmes de fermeture, Systèmes implicatifs, base d'implications, treillis de Galois / treillis des Concepts, extraction de connaissance, représentation de connaissance, datamining.
Sujet de thèse :
Algorithmique combinatoire : Cliques, Bicliques et Système d'implications
Thèse soutenue le 8 décembre 2005, sous la direction du professeur Lhouari Nourine
Le manuscrit est disponible en ligne. Un résumé des mes travaux de thèse est disponible sur cette page.
Mes activités de recherche s'articulent autour de l'énumération de familles d'objets combinatoires obtenus à partir d'une structure discrète. De part leur utilité en représentation et extraction de connaissance (Analyse formelle de concept, datamining), les objets combinatoires étudiés sont les cliques maximales d'un graphe, les bicliques maximales d'un graphe biparti (ou de façon équivalente, la famille des concepts d'un contexte binaire, la famille des itemsets fermés d'une relation) et les implications contenues dans une base canonique minimum (Base de Guigues-Duquenne).
Mes travaux de thèses ont apporté deux contributions principales :
Alors que de nombreuses études comparent les structures de données utilisées par les algorithmes d'énumérations des bicliques (i.e les itemsets fermés en datamining), nous avons privilégié une étude du comportement de ces algorithmes, indépendamment de la structure de donnée sous-jacente. Nous avons défini le graphe des transitions des cliques maximales (resp. bicliques maximales) d'un graphe G. Il s'agit d'un graphe orienté dont les cliques maximales de G sont les sommets, et ou il existe un arc d'une clique A vers une clique B s'il est possible de passer de la première à la seconde par une fonction de transition simple. Par simple, nous entendons une fonction qui transforme A en B en temps polynomial en la taille du graphe, et utilisant des opérations ensemblistes classiques, comme l'union ou l'intersection.
Ce graphe de transition nous permet de comparer le comportement de plusieurs algorithmes existants. Une transformation psimple permettant de passer du problème de l'énumération des bicliques maximales d'un graphe biparti à celui de l'énumération des cliques maximales d'un graphe, il permet aussi de rapprocher des algorithmes conçu initialement pour l'un ou l'autre de ces problèmes. Par exemple, l'agorithme de (Tsukiyama & al 77) pour l'énumération des cliques maximales, et celui de (Ganter 84) pour l'énumération des ensembles fermés d'un système de fermeture (en bijection avec les bicliques maximales d'un graphe biparti) ont le même comportement
Un système de fermeture peut être représenté par une famille d'implications. De fait, plusieurs familles d'implications peuvent représenter le même système de fermeture (une implication pouvant se dériver d'autres via les axiome d'Armstrong). Parmis les différentes familles d'implications représentant un système de fermeture, il en existe une, canonique, possédant un nombre minimum d'implications : La base de Guigues-Duquenne
Un système de fermeture peut aussi être représenté par la famille de ces éléments irréductibles. Il n'existe pas actuellement d'algorithme polynomial (au sens des algorithmes d'énumération, i.e polynomial en temps total) prenant en entrée la famille des éléments irréductibles (dont une relation binaire - par exemple la relation clients / articles dans le panier - est un sur-ensemble quelconque) et donnant la famille des implications de la base de Guigues-Duquenne en sortie. Ce problème est important dans plusieurs champs applicatifs (extraction de connaissance, base de données, théorie des graphes)
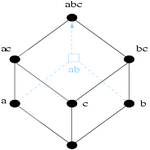
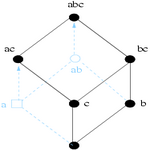
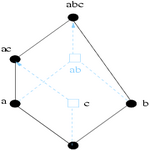
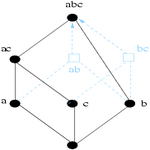
En considérant respectivement le système de fermeture, les éléments irréductibles de ce système et la base d'implications associés, nous avons donné les conditions nécessaires et suffisantes pour que l'ajout d'une implication unitaire (prémisse réduit à un singleton) ne remette pas en cause la famille des implications non unitaires de la base de Guigues-Duquenne.
D'autre part, avec la notion d'éléments clones, nous avons montré qu'une partie de l'explosion combinatoire dans le nombre d'implications de la base de Guigues-Duquenne est du (à l'absence de / aux) implications unitaires.
Ces travaux peuvent être utilisés comme pré-traitement sur les données, ou de façon à perturber l'entrée pour la rendre plus facilement exploitable (incrémentalité)
Nous avons définit H(G), le graphe de transition des cliques maximales d'un graphe G. Il nous reste à étudier quelles sont les propriétés de ce graphe, dans le cas général, mais aussi pour des classes particulières de graphes. On peut par exemple se demander si ce graphe est hamiltonien et dans quelle proportion l'étiquetage des sommets influe sur sa structure. En effet, les transitions entre cliques sont basées sur des propriétés lexicographiques. Aussi une variation dans l'étiquetage des sommets va nous permettre d'obtenir de nouveaux graphes de transitions. D'autre part, on peut aussi chercher à modifier la façon d'obtenir une transition (autres fonctions de transitions) entre deux cliques pour obtenir des variantes de ce graphe.
Pour l'énumération des implications d'une base minimum, nous avons mis en avant des propriétés intéressantes (éléments clones, influence des implications unitaires) mais il ne s'agit que du début d'une étude poussée des bases d'implications minimum. Nous espérons mettre à jour d'autres propriétés intéressantes dans les travaux à venir, pour finalement aboutir à un algorithme d'énumération polynomial de telles bases.
Enfin, tester si l'ajout d'une implication unitaire est possible sans modifier les implications non unitaires se fait en temps polynomial, de même que le calcul de la nouvelle famille d'éléments inf-irréductibles. Il nous faut maintenant développer une algorithmique efficace pouvant être effectivement implantée pour des cas réels d'utilisation.
De même, un prototype d'algorithme générique d'énumération des cliques et bicliques maximales peut être envisagé à partir du graphe de transition, permettant le test et le développement rapide de nouvelles variantes d'arborescence ou de parcours.
De façon plus générale, les techniques mises en oeuvre peuvent être utilisées pour d'autres objets combinatoires : on pourra étudier le coté plus structurel d'un problème, par exemple pour en faire diminuer la combinatoire, comme nous l'avons fait pour les implications d'une base minimum, ou le coté plus algorithmique en s'appuyant sur une littérature abondante et sur l'expérience acquise sur le problème de l'énumération des cliques et des bicliques maximales d'un graphe.
Les systèmes de fermeture, sous différentes formes (systèmes d'implications, treillis, éléments inf-irréductibles) sont au coeurs de plusieurs problèmes de recherche, dans le domaine du datamining (énumération des clés d'une base de données), de la théorie des graphes (transversaux minimaux d'un hypergraphe), de la logique (dualisation des fonctions booléennes monotones), des ensembles ordonnés (via le système de fermeture correspondant à des classes particulières de treillis) Les études menées sont autant d'outils permettant d'aborder des problèmes de divers domaines en utilisant les propriétés des systèmes de fermeture.
Enfin, notons que ces problèmes sont l'occasion d'utiliser des outils théoriques proches des mathématiques discrètes, lors de l'étude de propriétés structurelles, mais aussi de nombreuses méthodes algorithmiques (structures de données particulières, codage de l'entrée du problème, type de parcours, ...) afin d'obtenir une implémentation efficace pouvant servir en utilisation réelle pour des problèmes industriels (passage à l'échelle).